このページではポートフォリオと相関係数の関係性について解説します。
投資のリスクとリターンに関係するので、ポートフォリオと相関係数を理解しておくことは大切です。
投資で成功するために必要不可欠な知識と言っても過言ではありません。
専門家レベルの知識は必要ではないとしても、ポートフォリオと相関係数について大まかに把握しておくべきでしょう。
ポートフォリオとは
ポートフォリオとは「どのような金融商品を、どのくらい保有しているのか」という内訳を具体的に示したものです。
ポートフォリオとは、金融商品の組み合わせのことで、特に具体的な運用商品の詳細な組み合わせを指します。「ポートフォリオを組む」ということは、どのような投資信託を購入しようか、株はどの銘柄で何株ほど持つか、などの検討をするという意味です。
SMBC日興証券HP
資産運用という大枠でポートフォリオを述べると様々な金融商品が対象となります。
- 現金
- 株式
- 投資信託
- 債券
- 外貨
- 不動産
- 金
どんな金融商品を使ってポートフォリオを組んだとしても、相関係数は投資成績に深く関係してきます。
相関係数とは
相関係数とは2つの変化するデータ間に、どのような関係性があるかを数値的に示したものです。
相関係数は、2つの確率変数の間にある線形な関係の強弱を測る指標である。相関係数は無次元量で、-1以上1以下の実数に値をとる。相関係数が正のとき確率変数には正の相関が、負のとき確率変数には負の相関があるという。また相関係数が0のとき確率変数は無相関であるという。
Wikipedia
例えば、「商品Aが好調なら、商品Bは不調になる」というようなデータがあったとき、商品Aと商品Bの相関係数は○○と示すことができます。
このように2つのデータがどのように関係して動くのかを、わかりやすく数字で表すのが相関係数の役目です。
ポートフォリオと相関係数の理解は資産運用において重要
あなたのもっている株式Aと株式Bはどのように関係して動くのか。
あなたのもっている投資信託と不動産はどのように関係して動くのか。
適当に資産運用をするのではなく、ポートフォリオの相関係数を意識することが大切となります。
ポートフォリオの基本は分散投資です。
なぜなら、分散投資はリスクを下げながら、より良いリターンを得ることができるから。
しかし、投資した商品の相関係数によっては分散投資の効果が薄まってしまうのです。
例えば、あなたは株式A、B、C、Dに分散投資しているとします。
「株式Aが好調なとき、株式B、株式C、株式Dも好調になる」という関係性があったとき、株式A~Dは同じ方向に値動く傾向があるとわかります。
つまり、株式Aが不調のときは、株式B・C・Dも同じように不調になるのです。
上記の関係性を株式A、B、C、Dの相関は強いと言います。
株式Aが不調になると、すべての株式が同じように不調になるので、株式A~Dへの分散投資は効果が弱いです。
株式Aの不調が連鎖していき、株式B・C・Dも暴落して、誰もポートフォリオを支えてくれないので、あなたの資産は大きなダメージを受けます。
分散投資でリスクを下げるためには、ポートフォリオと相関係数を計算してポートフォリオを組む必要はあるのです。
リスクを分散するために、商品がどのように関係して動くのか(相関係数)を考慮してポートフォリオを組みましょう。
関連記事:初心者が株で失敗した例を画像付きで紹介
ポートフォリオと相関係数の関係性
ポートフォリオと相関係数の関係性を表にまとめました。
投資本のベストセラーである「ウォール街のランダム・ウォーカー」より引用しています。
| 相関係数 | リスク分散効果 |
| +1.0 | 効果なし |
| +0.5 | 緩やかなリスク低下 |
| 0 | かなりのリスク低下 |
| -0.5 | ほとんどのリスク低下 |
| -1.0 | すべてのリスク消滅 |
表をみると、相関係数が低いほどリスクを下げる効果は強いことがわかるでしょう。
相関係数は+1から-1の間に収まるのですが、相関係数が+1のことを完全に正の相関と言い、相関係数が-1のことを完全に負の相関と言います。
相関係数がプラス1のことを完全に正の相関と言い、2つの市場が完全に同じ動きをする(同時に上下する)場合を意味します
相関係数がマイナス1のことを完全に負の相関と言い、2つの市場が完全に逆の動きをする(片方が上がれば、一方は下がる)場合を意味します
完全に負の相関にある投資商品に分散投資することができれば、投資のリスクをほとんど消すことが理論上は可能なのです。
株式ポートフォリオの相関係数が負の相関でも安心できない
株式ポートフォリオを組むときには負の相関を意識して分散投資をすることが大切です。
お互いが逆の動きをする株式を組み合わせてポートフォリオを組みましょう(異なる値動きをする株式Aと株式Bを組み合わせるなど)
しかし、株式ポートフォリオの相関係数が負の相関でも安心はできません。
なぜなら、株式において分散投資では低下しないリスクがあるからです。
現実の世界では分散投資によってもすべてのリスクを取り除くことはできない。なぜなら、株式というものは程度の差はあっても、同じ方向に上げ下げする傾向があるからである。したがって、分散投資はすべてのリスクではなく、ある程度のリスク低減をもたらすことになる。
ウォール街のランダム・ウォーカー【第10版】
株式というものは、ある程度は同じ方向に上下するので、分散投資によってリスクをすべて取り除くことはできません。
株式ポートフォリオの負の相関には限界がある
株式ポートフォリオの相関係数が負の相関でも安心できない理由は、株式の分散投資には限界があるからです。
株式はどれだけ分散しても、ある程度は同じ値動きをするという性質があるのです。
株式には市場リスクと非市場リスクがあります。
【市場リスク】
株式市場全体の変動によって生まれるリスク(例:ブラックマンデー、リーマンショックなどの世界的不況によって株価が下落する)
【非市場リスク】
個々の株式・企業特有の要因によって生まれるリスク(例:東日本大震災の原子力発電所事故によって東京電力の株価が下落する)
非市場リスクは分散投資で低下しますが、市場リスクは分散投資で低下しないのです。
例えば、東日本大震災による東京電力の株価下落は、東京電力以外の株式に分散投資していれば、ダメージを相殺することができます。
しかし、リーマンショックのような世界的不況では、すべての株式が同じように下落するので、分散投資をしていてもダメージを相殺できません。
株式投資をしているかぎり、市場リスクから逃れることができないので、株式ポートフォリオの負の相関(分散投資)には限界があるのです。
関連記事:【投資に興味ない人が多い理由】貯金を優先してしまう日本の実態
株式ポートフォリオの分散が絶対に必要な理由
株式ポートフォリオの分散投資には限界があると言いましたが、それでも分散投資は絶対に必要なのです。
なぜなら、分散投資によって非市場リスクを取り除くことができるから。
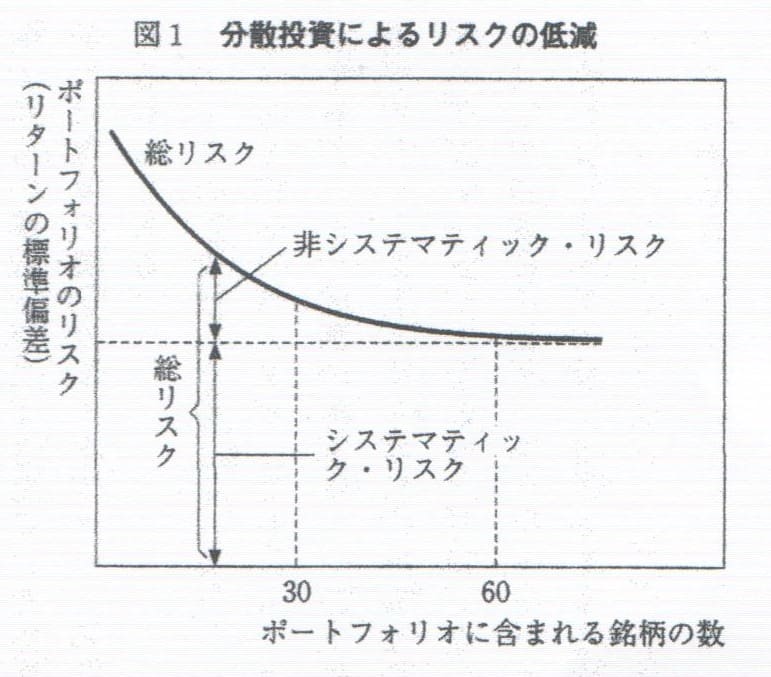
上図は分散投資による市場リスク(システマティック・リスク)と非市場リスク(非システマティックリスク)の関係を示したものです。
横軸のポートフォリオ銘柄数が増えると、実線は右肩下がりとなっており、非市場リスク(横点線の上部)が低下しています。
しかし、ポートフォリオの銘柄数が増えても、市場リスク(横点線の下部)は変わっていません。
つまり、非市場リスクは分散投資によって取り除くことができるが、市場リスクは分散投資では取り除くことができないということ。
そして、「投資家が非市場リスクを取ることに意味はない」と言われています。
投資家が非市場リスクを負うことに対してリスク・プレミアムが支払われると考えるべき理由はない。総リスクのうちプレミアムによって報われるのは、あくまでも分散投資によっても除去できない市場リスクの分だけである。
ウォーカー街のランダム・ウォーカー【第10版】
「大きなリターンを得るためには大きなリスクを取る必要がある」と言われますが、大きなリスクというのは市場リスクのことです。
投資家は分散投資によって非市場リスクを取り除き、どれほどの市場リスクを取るのかを考えて投資を実行することが大切です。
関連記事:庶民が投資でお金を増やす方法!一般家庭にもできる資産運用
ポートフォリオの相関係数が正の相関でも効果はある
ポートフォリオと相関係数において重要なことは「正の相関でも分散の効果はある」ということです。
さきほど紹介した表を見ると
| 相関係数 | リスク分散効果 |
| +1.0 | 効果なし |
| +0.5 | 緩やかなリスク低下 |
| 0 | かなりのリスク低下 |
| -0.5 | ほとんどのリスク低下 |
| -1.0 | すべてのリスク消滅 |
相関係数プラス0.5の正の相関でも「緩やかなリスク低下」をしていることがわかります。
つまり、相関係数1の完全な正の相関でなければ、分散投資には意味があるということです。
完全に正の相関でないかぎり、分散投資すればリスク低下に役立つ可能性があります。
グローバル社会では相関係数が高まって、分散投資の効果が薄まってきたと言われますが、完全な正の相関には遠いので投資初心者はとにかく分散投資です。
まとめ
ポートフォリオとは金融商品の内訳であり、相関係数は金融商品がどのように関係しているかを示したものです。
金融商品を組み合わせてポートフォリオをつくるとき、以下のポイントを自分なりに計算して考えましょう。
- 相関係数が高いと分散投資の効果は弱い
- 相関係数が低いと分散投資の効果は強い
分散投資はリターンを維持しながらリスクだけを下げることができるので利用しない手はありません。



コメント