このページでは長期投資でリスク低減しない理由を解説します。
長期投資によってリスクは低減するという言葉にはカラクリがあります。
有名な投資本では長期投資のデータを載せて、長期投資でリスクは低減すると示されていますが、実際のところは長期投資でリスクは低減しません。
ちなみに、私は長期投資によって元本割れのリスクはたぶん下がると思っています。
長期投資はリスクを下げないけど、元本割れのリスクは下げるとはどういうことでしょうか。
【結論】長期投資でリスクは低減しない
結論として長期投資でリスクは低減しません。
投資におけるリスクとは「リターンのばらつき」を言います(基本的にリターンのばらつきは標準偏差で表します)
ここでは「投資リスク=リターンのばらつき=標準偏差」と解釈しても問題ありません。
では、長期投資をすれば投資商品やポートフォリオのリスクは低減するのでしょうか?
例えば、あなたが投資信託Aを運用しているとします。
- 投資信託Aを5年運用した後にリーマンショック級の大暴落が訪れた場合
- 投資信託Aを30年運用した後にリーマンショック級の大暴落が訪れた場合
上記2つのケースではどちらが損失は少ないと思いますか。
おそらくですが、上記2つのケースともに大きな損失を抱えるはずです。
どれだけ長期運用をしようが、同じ商品に投資をしているのだから、損失のばらつきは同じになります。
30年運用したポートフォリオであれば、リーマンショック級の暴落がきても大丈夫という考え方は間違いです。
長期投資でポートフォリオAがポートフォリオA+に変化しないかぎり投資リスクは変化しません。
長期投資でリスクは低減するという主張
長期投資でリスクは低減するという理解が大きく広がったのは、バートン・マルキールの著書「ウォール街のランダム・ウォーカー」の影響だと思います。
ウォール街のランダム・ウォーカーでは、株式投資のリスクについて以下のように述べられています。
株式を「長期間」保有し、一度買ったら多少の価格変動があっても我慢して持ち続けるという基本方針を貫ければ、リスクの全部ではないが、かなりの部分を減らすことができる。
引用:ウォール街のランダム・ウォーカー【第10版】
上記の文章から長期投資でリスクを減らすことができると解釈するのは無理ありません。
では、実際はどうなのでしょうか?
バートン・マルキールの長期投資でリスクの全部ではないが、かなりの部分を減らすことができるという主張は下のグラフを根拠にしています

上図はS&P500指数の年平均リターンのばらつきをグラフにしたものです。
グラフを見ると、投資期間が長くなるにつれて棒グラフの長さは短くなり、年平均リターンのばらつきが小さくなっています。
最高リターンと最低リターンの差(ばらつき)が小さくなっており、投資リスクが低下しているように見えます。
以下より詳しく解説していきます。
【徹底解説】長期投資でリスクは低減しない理由
長期投資でリスクは低減しないのでウォール街のランダム・ウォーカーの主張は正確ではありません。
正確でない理由を示すには、ウォール街のランダム・ウォーカーでバートン・マルキールが示したグラフの意味を説明する必要があります。
- ウォール街のランダム・ウォーカーのグラフの作り方
- グラフは標準偏差(投資リスク)を示さない
- 長期投資で元本割れの確率が下がる
遠回りになりますが、上記の流れで説明していきます。
ウォール街のランダム・ウォーカーの誤解をぜひご覧ください。
ウォール街のランダム・ウォーカーのグラフの作り方
本当にリスクが小さくなっているのかを理解するためには、ウォール街のランダム・ウォーカーのグラフの作り方を知る必要があります。
「株式投資の投資期間と年平均リターンのちらばり方(1950~2009年)」というグラフはどうやって作られているのか。
投資期間10年を例に考えます。
【ステップ①】
S&P500の1950~2009年の各年間リターンから、連続する10年間の年平均リターンを求める。
S&P500のデータを使って計算します。
・1950年から1959年の連続する10年間の1年平均リターンを求める(濃い緑)
・1951年から1960年の連続する10年間の1年平均リターンを求める(濃い青)
・1952年から1961年の連続する10年間の1年平均リターンを求める(濃い赤)
・1953年から1962年の・・・・・・
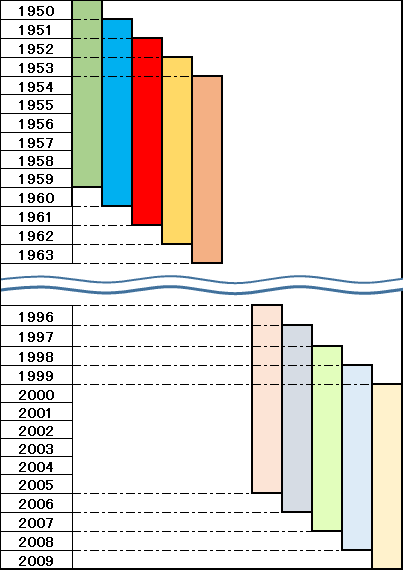
1950~2009年の全期間において、図のように1年ずつズラしながら、S&P500の連続する10年間の1年平均リターンを求めます。
【ステップ②】
1年平均リターンの平均値を求める。
①によって求められた連続する10年間の1年平均リターンの平均値を求めます。
ウォール街のランダム・ウォーカーのグラフでいうと、グラフ中央にある黒い楕円のことです。
【ステップ③】
1年間平均リターンの最大値・最小値を求める。
①によって求められた連続する10年間の1年平均リターンから最大値と最小値をピックアップします。
そして、平均値と最大値・最小値でグラフを作れば完成。
上記の手順によって、ウォール街のランダム・ウォーカーのグラフは作られたのです。
今回は10年間を例に挙げましたが、グラフでは連続する5年間、連続する15年間、連続する20年間、連続する25年間でも1年平均リターンを求めています。
グラフは標準偏差(投資リスク)を示すものではない
結論を先にいうと、ウォール街のランダム・ウォーカーのグラフは標準誤差を表しています。
投資リスクを表す指標は標準偏差です。
標準誤差?
標準偏差?
微妙に違います。
標準誤差には広義・狭義とあるみたいですが、標本平均の標本分布の標準偏差のことを標準誤差と言います。
標準誤差=標本平均の標本分布の標準偏差
つまり、標準誤差は標本平均のばらつきを表す指標なのです。
ウォール街のランダム・ウォーカーのグラフでいうと、標本平均は1年平均リターンのことです。
つまり、グラフは1950年から2009年の期間において、標本平均(1年平均リターン)が、どの程度ばらつくのかを調べた「標準誤差のグラフ」なのです。
そして、知っておくべきことは、標準誤差の数値は標本平均のサンプル数を増やすと、ばらつきが小さくなるということです。
標準誤差の計算式は以下のとおり。
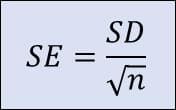
標準誤差はSE
標準偏差はSD
nは標本平均のサンプル数
ウォール街のランダム・ウォーカーのグラフでいうとnは年数です。
計算式を見るとわかりますが、標準誤差は標準偏差を標本平均のサンプル数の平方根で割った数値です。
つまり、標本平均のサンプル数が増えるほど、標準誤差は小さくなるということです。
グラフは連続する投資期間をピックアップして、各年平均リターンから標準偏差を求めて、その値を年数の平方根で割ると計算できる標的誤差を表しています。
標準誤差という指標において、投資期間が長くなると「年平均リターンのちらばり方」が小さくなるのは当たり前のことです。
5年、10年、15年、20年、25年と投資期間が増えると、ばらつきが当たり前に小さくなります。
長期投資によって元本割れの確率は下がる
ウォール街のランダム・ウォーカーのグラフは、長期投資で標準誤差が下がるという意味では正しいです。
しかし、投資リスクは一般的に標準偏差なので、投資リスクが下がるという意味では間違いです。
ウォール街のランダム・ウォーカーのグラフは元本割れの確率が下がっていることを表しています。
投資期間25年では棒グラフが短くなっており、リターンのちらばりは小さくなっているのです。
そして、投資期間25年のグラフはプラスの範囲に収まっており、S&P500に25年間投資を続けていれば元本割れはしなかったということを表しています。
ただし、これはS&P500のパフォーマンスが素晴らしいからこそです。
期待リターンがプラスの場合、運用期間が長くなると元本割れする確率は小さくなります。
S&P500が長期的に右肩上がりで成長していき、全体的にプラスパフォーマンスで推移したからこそ、25年のグラフはプラスの範囲で収まっているのです。
マイナスパフォーマンスの割合によっては元本割れをしていたかもしれません。
まあ、私たちは期待リターンがプラスだからこそ投資をするわけで、期待リターンがマイナスの場合は投資しないのですが。
長期投資でリスクは上がるという主張
経済評論家である山崎元さんは、長期投資でリスクは下がるという主張に否定的な記事を書かれています。

山崎元さんは1年間と5年間の投資を比較するとき、両者の運用資産金額で比較しなければいけないと主張され、記事内で以下のように結論づけています。
運用期間が長期化すると、資産額の期待値からの現実の運用資産額のばらつきは拡大していくのであり、不運な場合のがっかりの大きさは運用期間と共に拡大すると考えるべきだ。
引用:楽天証券HP トウシル
経済評論家である山崎元さんは、長期投資によってリスクは上がるとおっしゃっています。
- 現実の運用資産額のばらつきは拡大していく
- 不運な場合のがっかりの大きさは運用期間と共に拡大する
上記2箇所が山崎元さんの長期投資でリスクは上がるという意見です。
資産金額が増えると最高・最低リターンの差は拡大する
長期投資でリスクは上がる理由をウォール街のランダム・ウォーカーのグラフを使って解説します。

グラフはS&P500の年平均リターンの最高値・最低値を表しています。
あなたがS&P500に100万円投資したと仮定して(為替は無視)、投資期間1年と25年の最高リターンを最低リターンを比べます。
【投資期間1年】S&P500に100万円投資
投資期間1年では最高値がプラス52.62%で最低値がマイナス37.%です。
最高・最低値の投資成績を計算すると以下のとおり。
最高:100×(1+0.5262)=152.62
最低:100×(1-0.37)=63.0
投資元本は最高で152万6200円、最低で63万円となります。
最高と最低の金額差は89万6200円です。
【投資期間25年】S&P500に100万円投資
投資期間25年では最高値がプラス17.24%で最低値がプラス7.94%です。
最高・最低値の投資成績を計算すると以下のとおり。
最高:100×(1+0.1724)25=5332
最低:100×(1-0.0794)25=675
投資元本は最高で5332万円、最低で675万円となります。
最高と最低の金額差は4657万円です。
投資期間1年と25年では最高リターンと最低リターンの運用金額差が大きく違ってきます。
投資期間25年では最高と最低に4657万円という大きな差が生まれる可能性があるのです。
投資期間が長くなることによって、運用資産金額のばらつき(最高と最低の差)が大きくなっていることを意味しています。
つまり、現実の運用資産額のばらつきは拡大していくということです。
損失額は運用期間とともに増えていく
標準偏差(リスク)10%の投資商品Aがあるとします。
投資商品Aのリターンをゼロと仮定して、以下2つのケースを比較します。
- 1年間の投資でマイナス1標準偏差の成績となるケース(短期投資)
- 5年間の投資でマイナス1標準偏差の成績が5年連続して続くケース(長期投資)
1年間の投資でマイナス1標準偏差(マイナス10%)の成績となった場合、運用資産金額は元本の90%に減ってしまいます。
1年目:100%×(1-0.1)=90
5年間の投資でマイナス1標準偏差(マイナス4.47%)の成績が5年連続して続いた場合、運用資産金額は元本の約79.54%に減ってしまいます。
1年目:100%×(1-0.0447)=95.53
2年目:95.53×(1-0.0447)=91.25
3年目:91.25×(1-0.0447)=87.17
4年目:87.17×(1-0.0447)=83.27
5年目:83.27×(1-0.0447)=79.54
連続する5年間の年平均リターンのばらつき(標準誤差)は4.47%と計算できます。年平均リターンのばらつきは標本平均の標本分布の標準偏差(標準誤差)であり、年平均リターンの標準偏差を年数(サンプル数)の平方根で割って計算するため数値は小さくなります。
上記のケースをまとめると以下のとおり。
- 1年間の投資で元本は90%に減った
- 5年間の投資で元本は79%に減った
結果的にどちらの投資が高リスクだったかは一目瞭然です。
つまり、投資期間を長くしたとしても、マイナスリターンが続けば損失は広がります。
上記の例が山崎元さんの主張である「不運な場合のがっかりの大きさは運用期間と共に拡大する」の意味するところです。
長期投資したからといって、損失が増えないわけではありません。
長期投資はリスクを下げるどころではなく、マイナスリターンが継続すれば資産損失は増え続けます。
まとめ
投資におけるリスクとは「リターンのばらつき」なので、長期投資によって投資リスクが低減するとは言えません。
なぜかというと、同じ商品に投資しているかぎり、その商品の利益・損失のばらつきは変わらないからです。
長期投資によって株式Aが株式Bに変化すれば投資リスクは変わりますが、そんなことは絶対にありえません。
資産運用で失敗しないためにも、投資リスクについてはしっかりと理解しておきましょう。
最後に山崎元さんのお言葉で終わりたいと思います。
株式、債券、あるいは不動産のようなもので資金を運用する場合、これらへの投資は、資金を提供している期間、生産活動に資本を提供し、その果実を得ようとする行為だ。株式を例に取るとして、いかなる企業であっても利益を上げるために時間が掛かるのは当然であり、長期投資とは、その間資本を提供し続けることを意味する。投資の本質を生産活動への資本の提供と考えるなら、より長期で投資し続けることの意味は大きい。
引用:楽天証券HP トウシル
- 長期投資のメリットを解説
- 長期投資のデメリットを解説
- 長期投資は儲からないの嘘と本当を解説
- 長期投資でリスク低減しない理由をわかりやすく解説
- 長期投資の失敗をブログで公開!過去の迷走ぶりをありのままに



コメント