投資信託のリスクと標準偏差をわかりやすく解説

このページでは投資信託のリスクと標準偏差について解説します。

投資信託のリスクを理解するうえで、標準偏差の知識はとても大切なのです。

「標準偏差という文字からして難しい」と戸惑っている投資家は多いと思います。

しかし、標準偏差を理解しないまま投資信託を運用していると、大きな損失を抱えてしまうかもしれません。

標準偏差を理解してこそ、しっかりとした資産運用ができるのです。

標準偏差は投資信託のリスクを表す指標

標準偏差とは投資リスクの指標であり、投資信託のリターンのばらつきを表すものです。

私は標準偏差の考え方に触れたとき「標準偏差はリスクの指標？」「標準偏差はリターンのばらつきを表す？」というように頭を悩ませました。

標準偏差という言葉が、いろいろな言い回しで説明されるから、頭が混乱するのです。

投資信託においては「標準偏差＝リスク＝リターンのばらつき」と解釈しても問題はありません。

標準偏差は「〇％」のように数字で表すことができ、数字が大きくなるとリスク（リターンのばらつき）は大きくなるのです。

下図の証券Aと証券Bを例にすると

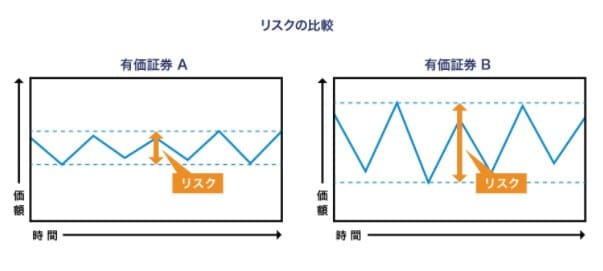
証券Aは標準偏差が小さい、証券Bは標準偏差が大きいと判断できます。

なぜなら、証券Aはリターンのばらつきが小さくて、証券Bはリターンのばらつきが大きいから。

言いかえると、証券Aはリスクが小さい、証券Bはリスクが大きいということです。

上記のように、標準偏差がいろいろな言い回しで説明できるからこそ、標準偏差の仕組みを知らない投資家は混乱するのだと思います。

以下より、標準偏差をわかりやすく説明していきます。

投資信託のリスクと標準偏差に疑問を感じている投資初心者はぜひ読み進めてください。

標準偏差をわかりやすく解説

標準偏差とはデータのばらつきを示す指標のことです。

偏差値・視聴率など統計データを表すときにも使われています。

投資初心者の方は標準偏差の概要から理解することが大切です。

以下より、標準偏差をわかりやすく解説していきます。

【7人の投資家しかいない株式市場の話】

まず、世界に7人の投資家（A、B、C、D、E、F、G）しかいないと仮定します。

そして、7人の投資家は3つの相場（相場①、相場②、相場③）を経験しました。

相場①、②、③の7人平均リターンはそれぞれ8％でした。

そのなかで、Aさんは3つの相場とも10％のリターンを上げました。

このAさんの結果を聞いて、「Aさん、すごい！」と感じる人は多いのではないでしょうか。

7人の平均を上回ったのだから、Aさんはすごいはずです。

しかし、相場全体の結果によっては「Aさん、すごい！」とは言えません。

それぞれの相場における7人の投資家の結果によっては違った見方になります。

例えば、それぞれの相場の結果が下記のようだとしたらどうでしょう。

【相場①】

• A：10％
• B：12％
• C：1％
• D：15％
• E：2％
• F：15％
• G：1％

相場①は成績が良い人と悪い人で分かれています。

Aさんは平均を上回っていますが、Aさんより成績の良い投資家（D、F、B）が3人もいて、順位でいうとAさんは第4位です。

他3人の投資家（C、E、G）の成績が極端に悪く、全体平均を大幅に引き下げています。

相場①の結果は「Aさん、すごい！」というより、「Aさんは普通・・」という印象のほうが強いのではないでしょうか。

【相場②】

• A：10％
• B：8％
• C：3％
• D：5％
• E：3％
• F：3％
• G：24％

相場②は成績が極端に分かれています。

Aさんは平均以上の成績を上げており、順位でいうとAさんは第2位です。

ただ、Gさんがダントツの成績を上げているので、心から「Aさん、すごい！」とは言えません。

また、Bさんがそこそこのリターンを上げているので、Aさんの印象は薄れてしまいます。

そして、他の投資家（C、D、E、F）の成績が悪くて平均を押し下げているため、平均を超えたことを自慢できる相場ではないように思えます。

【相場③】

• A：10％
• B：8％
• C：6％
• D：8％
• E：8％
• F：8％
• G：8％

相場③は成績が拮抗しています。

Aさんの順位は第1位であり、「Aさん、すごい！」と言える相場でしょう。

他の投資家が平均以下なので、平均を超えることが難しかった相場であると解釈できます。

他の投資家が平均を超えていない相場で、ひとりだけ平均を超えたAさんはすごいのではないでしょうか。

上記の例から何が言いたいのかというと、平均8％という数字だけでは相場の背景が把握できないということです。

Aさんが平均以上の成績を上げたとしても、他の投資家の成績によっては評価が異なります。

つまり、成績の数字だけではAさんの評価がしっかりとできないのです。

そこで役に立つのが標準偏差です。

3つの相場の標準偏差を計算すると下記のようになります（端数切り捨て）

標準偏差はデータのばらつきを表すので、「どれだけばらつきのある相場だったか」を示すことができるのです。

相場①と②は標準偏差が大きいので、データのばらつきが大きいことを示しています。

それに対して、相場③は標準偏差が小さいので、データのばらつきが小さいことを示しています。

つまり、標準偏差というデータ加わることで、詳細な分析が可能となるのです。

• 相場①と②は標準偏差が大きいから、データのばらつきが大きいかもしれない
• 相場③は標準偏差が小さいから、ばらつきが小さいかもしれない

上記のような判断ができるので、ばらつきが少ない相場③で10％のリターンを上げたAさんのすごさがわかりやすくなります。

標準偏差でデータのばらつきを示すことによって、物事をより深く判断することができるのです。

投資信託をするうえで標準偏差の理解はなくてはならない

投資信託をするうえで標準偏差を理解しておくことは、投資家にとって最重要ポイントといっても過言ではありません。

なぜなら、標準偏差を理解している投資家だけが、適切な資産運用ができるからです。

投資信託のリスクを標準偏差という数字で表すことができると、投資家が投資方針や投資判断を考えるときに役立ちます。

「投資信託Aは標準偏差（リスク）が大きいから、リターンのばらつきは大きいだろうし、投資する際には注意しないといけない」

「投資信託Bは標準偏差（リスク）が小さいから、リターンのばらつきは小さいだろうし、安心して投資できる」

「今は相場が不安定だから、リスクの小さい投資信託Bの割合を増やして投資しよう」

投資家は標準偏差を参考にしながら、上記のような判断ができるようになります。

標準偏差を考慮して、自分が受け入れられるリスク（リスク許容度）にあわせて、投資信託を選ぶことは資産運用の鉄則です。

投資信託のリスク（最大損失額）は標準偏差で把握できる

標準偏差を活用すれば、自分がしている投資によって、どれくらいの最大損失が発生するかを把握することができます。

最大損失額の理解は初心者に限らず、すべての投資家にとって必須です。

標準偏差で最大損失額が把握できる仕組みについて、以下の3ステップで解説します。

• 標準偏差と正規分布の関係性とは
• 標準偏差でリターン発生確率がわかる
• 標準偏差から投資信託の最大損失額が計算できる

最大損失額の計算方法をすぐに知りたい方は読み飛ばしてください。

標準偏差と正規分布の関係性とは

さきほど、標準偏差の解説のところで、7人の投資家の平均リターンを例に挙げました。

例では7人のデータでしたが、これが1000人、2000人の投資家の平均リターンとなると、データの分布にある特徴が出てきます。

それが正規分布です（下図）

1000、2000、3000というように、データの数が膨大になると、そのデータの分布は図のように「つり鐘型」になっていきます。

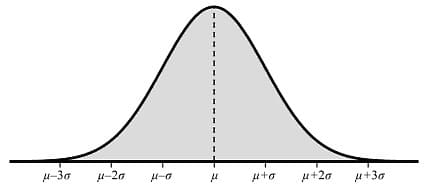
※図の記号は、μ（ミュー）は平均値、σ（シグマ）は標準偏差です。

図を見ると、μ（平均値）の分布が一番多いです。

そして、平均値から左右対称に

σ（1標準偏差）
2σ（2標準偏差）
3σ（3標準偏差）

と分布が減っていることがわかります。

このような「つり鐘型」のデータの分布が正規分布の特徴です。

学校のテストを例に挙げるとイメージしやすいと思います。

学校のテストでは、ほとんどの生徒が平均点くらいの成績を残しますが、数名の生徒が桁外れに良い成績を、数名の生徒が桁外れに悪い成績を残すのです。

つまり、統計データの数が多くなると、平均値の分布が一番多くなって、平均から大きく外れるほど分布は少なくなっていくのです。

正規分布の特徴が投資信託の最大損失額の計算に必要となります。

標準偏差でリターンの発生確率がわかる

データの分布が正規分布の形をしていた場合、標準偏差を使ってデータが含まれる確率を計算できるのです。

データの分布が正規分布なら、以下の法則が成り立つことが分かっています。

上記の法則は「68％95％ルール」とも言います。

データの総数が1000を超えた分布は、正規分布に近づくケースが多く、「68％95％ルール」は投資信託のリスクの理解にとても役に立ちます。

大まかなイメージとしては以下のとおりです。

文章ではわかりにくいと思うので、正規分布表を使って説明します。

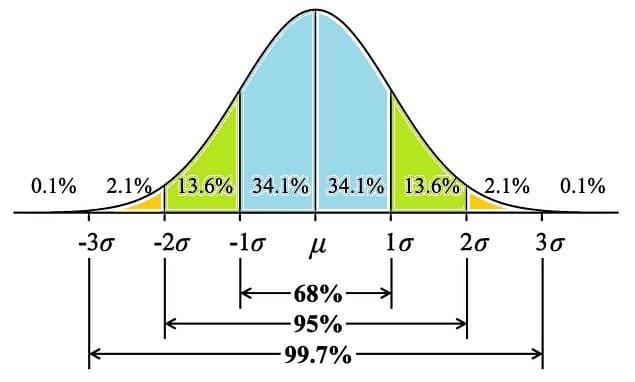
※図の記号は、μ（ミュー）は平均値、σ（シグマ）は標準偏差です。

あるデータ分布が正規分布の場合、1σと－1σの間に約68％（上の矢印）が、2σと－2σの間に約95％（下の矢印）が含まれることを上図は示しています。

これを知っていると、投資信託のリターン発生確率を大まかに把握することができるのです。

簡単にまとめると以下のとおりです。

さらに言いかえると、リスク5％の投資信託の1年後の成績は以下の範囲に収まるということです。

• 68％の確率で期待リターン±5％
• 95％の確率で期待リターン±10％
• 99.7％の確率で期待リターン±15％

上記のように、標準偏差と正規分布の関係性は、個人投資家に有益な情報を与えてくれるのです。

標準偏差から投資信託の最大損失額が計算できる

正規分布の「68％95％ルール」を使えば、標準偏差と投資信託の期待リターンから、1年間のうちで予想される最大損失額を計算することができます。

投資の世界では2標準偏差を見ておけば、最悪の事態を想定できると言われています。

さきほどの正規分布でいうと発生確率は約95％なので、めったに起こらない最悪事態ということです。

最大損失額は投資金額、期待リターン、標準偏差を、以下の式に当てはめれば計算することができます。

投資金額 ×{期待リターン－(2×標準偏差)}

【計算例】
期待リターン4.5％、標準偏差12.2％の投資信託Aにあなたは100万円を投資するとします。

100万円×{4.5％－(2×12.2％)}
＝100万円×(4.5％－24.4％)
＝100万円×(－19.9％)
＝－19万9000円

つまり、1年後には最大19万9000円の損失になる可能性があるということです。

最大損失が想定できておらず、急に19万円の損失が発生した場合、投資初心者であればパニックになるでしょう。

しかし、「19万円の損失があるかもしれない」と想定できていると冷静に対処できるはず。

投資信託のリスク許容度を確認する意味をこめて、想定される最大損失額を把握しておくといいと思います。

最大損失額の把握は「お金は寝かせて増やしなさい／水瀬ケンイチ」で推奨されています。

書籍では投資リスクに関して、より詳しく書かれているので、投資初心者におすすめです。

関連記事：【インデックス投資の良書】お金は寝かせて増やしなさいのレビュー

まとめ

標準偏差を理解しておくと、より安全な資産運用ができますし、最大損失額の把握（リスク許容度の確認）は大切な作業だと思います。

標準偏差を理解しておかないと、いつか後悔するかもしれませんし、20～30年と投資を続けていくのであればなおさらです。

投資初心者の方は投資を始める前に標準偏差を理解しておくべきです。

そして、標準偏差と最大損失額が理解できたなら、投資基本方針を見直してみてもいいでしょう。

• 投資信託のリスクとリターンを解説
• 投資信託のリスクと標準偏差をわかりやすく解説
• 投資信託のリスクは低いという言葉に騙されてはいけない
• 投資信託のリスクを分散する簡単な方法を解説